Home

Le Jeu

Intelligence Artificielle

Screenshot

Télécharger

Intelligence Artificielle

Le projet

Le but de ce projet est de réaliser un jeu, le Tablut d'Hnefetafl, dans lequel nous intégrerons les connaissances d'intelligence artificielle.

Organisation du travail

Le projet peut être décomposé en plusieurs parties successives, nous avons :

• Choisi la structure du jeu pour les performances de l'intelligence artificielle.
• Modélisé le jeu, le plateau de jeu et les mouvements des pièces sur le plateau tout en étant cohérent avec notre structure de jeu.
• Programmé le jeu.
• Intégrer le programme de notre jeu avec une interface client, qui permettra alors de jouer une partie en réseau contre un autre joueur.
• Implémenté une Intelligence Artificielle en réfléchissant sur son algorithme ainsi que sur le choix de l'heuristique.

Nous allons détailler tous les points énumérés ci-dessus dans l'ordre d'apparition.

Structure du jeu

Introduction de la structure du jeu :

La structure du jeu est très importante à définir dès le départ. En effet, c'est sur celle-ci que nous allons nous baser dans toute la suite du projet et c'est elle qui sera un facteur déterminant pour pouvoir optimiser la vitesse de recherche du meilleur coup à jouer.

Après réflexion, nous avons choisi de prendre la structure du plateau détaillé par le schéma ci-dessous :

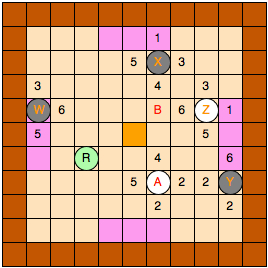
Chaque pion peut connaître les déplacements maximums qu'il peut réaliser dans toutes ses directions (en haut, à droite, en bas et à gauche). Nous avons ici des notions de direction et nous allons considérer dans toute la suite du rapport les notations suivantes :

• « La direction 0 » est la direction qui va vers le haut.
• « La direction 1 » est la direction qui va vers la droite.
• « La direction 2 » est la direction qui va vers le bas.
• « La direction 3 » est la direction qui va vers la gauche.
• « La valeur d'une direction i » est égale au déplacement maximal d'un pion dans la direction i choisie. C'est-à-dire que « la valeur d'une direction i » représente en fait un des quatre numéros qui sont représentés sur le schéma ci-dessus.

Complexité de la structure :

Cette structure de jeu n'est pas lourde à implémenter, car les distances sont faciles à mettre à jour. En effet, supposons que nous voulons déplacer le pion A vers la case B. Nous voyons alors que les calculs sont simples à effectuer :

• Le pion Y aura donc : valeur de sa direction 3 (nouvelle) = valeur de sa direction 3 (ancienne) + valeur de sa direction 3 de A + 1.
• Le pion X aura donc : valeur de sa direction 2 (nouvelle) = valeur de sa direction 2 (ancienne) - déplacement du pion A vers B.
• Le pion A aura donc : valeur de sa direction 0 (nouvelle) = valeur de sa direction 0 (ancienne) - déplacement du pion A vers B et valeur de sa direction 2 (nouvelle) = valeur de sa direction 2 (ancienne) + déplacement du pion A vers B.
• Le pion A calcule ses plus proches voisins dans les directions 1 et 3 et met à jour ses directions ainsi que les directions respectives des pions W (direction 1) et Z (direction 3).

Il n'y a donc pratiquement que des additions mises à part le fait que le pion A doit rechercher ses plus proches voisins dans les directions 1 et 3.
Le nouveau plateau sera donc :

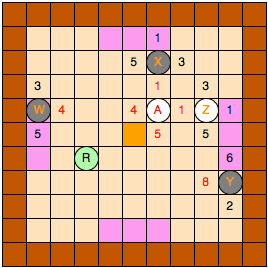
Avantages et inconvénients de la structure de jeu :

Après avoir trouvé notre structure, nous allons maintenant détailler les avantages et inconvénients d'un tel choix :

• L'avantage est de pouvoir connaître immédiatement tous les déplacements possibles de chaque pion. Nous pourrions aussi dire que ces valeurs pourront êtres utiles lors du calcul de l'heuristique.
• L'inconvénient majeur vient du fait que lorsque l'on déplace un pion, deux directions prendront du temps à être recalculé en cherchant les plus proche voisin. C'est cela qui peut faire perdre potentiellement de la puissance à l'algorithme de recherche du meilleur coup.

Modélisation du jeu

Avant de commencer à programmer le jeu, il nous a fallu en priorité faire un schéma UML du jeu afin de ne pas nous tromper dans le codage des éléments. Nous avons découpé le jeu en plus petits éléments ce qui nous a permis de décerner plusieurs objets différents constituant le jeu. Voici ci-dessous le schéma UML de notre programme :

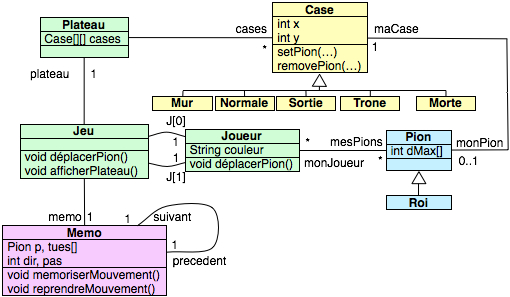
Programmation du jeu

ions et préconditions de la fonction.

DeplacerPion(Pion p, int dir, int pas) :
• préconditions :
-p = pion qui appartient au joueur courant et qui n'est pas mort

• dir = direction = {0, 1, 2, 3}
• pas > 0 : le déplacement est > 0 (la pièce bouge forcément)
• le déplacement est supposé être correcte, c'est-à-dire que l'on suppose que l'on a déjà fait les conditions nécessaires avant qui assurent que le mouvement ne sera pas incorrect.
  • postconditions :
• le pion p avance à la case voulue
• l'ancienne case se voit attribuer aucun pion.
• la nouvelle case se voit attribuer le pion p.
• les valeurs des quatre directions du pion p changent en accord avec le plateau.
• la valeur des pions voisins de l'ancienne position du pion p change.
• la valeur des pions voisins de la nouvelle position du pion p change.
  Mémorisation du mouvement d'un pion :

Cette fonction est sûrement la plus dure à mettre en place. Il fallait faire trouver un moyen de déplacer les pions, et de revenir en arrière.

Notre stratégie a été de faire une classe Memo. Le programme, à son lancement, va créer plusieurs classes Memo. Leur nombre est défini par l'utilisateur. Et le principe est d'utiliser les classes Memo comme si cela était une pile (de type FIFO). Nous allons donc maintenant détailler le fonctionnement de la fonction memoDepCapPion(Pion p, int dir, int pas) qui est chargé de gérer le déplacement du pion p et aussi les captures de pions engendrées par ce déplacement. Le mouvement complet sera alors enregistré dans la classe Memo.

memoDepCapPion(Pion p, int dir, int pas) va enregistrer les paramètres suivant :

• le pion p qui a été déplacé.
• la direction dans laquelle on a déplacé le pion.
• le nombre de pas effectué par le pion.
• les pions capturés après le mouvement du pion p dans le tableau tue[].

En fait, ce n'est pas tellement le fait de devoir mémoriser le déplacement du pion qui pose problème, car il suffira de faire le déplacement inverse à la restauration du mouvement (lorsque l'on appelle la fonction memoDefaireDepCapPion()). Le réel problème est de pouvoir retirer les pions capturés du plateau. Notre solution a consisté à inventer une nouvelle case du plateau qui est sous le nom de case Morte. Lorsqu'un pion X se fera capturé par un déplacement d'un pion ennemi, alors nous changerons le pointeur du pion X, qui était à l'origine vers une case du plateau, sur une case de type Morte. Chaque pion à son initialisation possède donc un pointeur vers une case de type Morte. Il y aura donc autant de cases mortes initialisées tout au long du jeu que de pions créés à l'initialisation d'une nouvelle partie. La case Morte permet juste de conserver les coordonnées et les valeurs maximales des quatre direction du pion qui est capturé

Maintenant, nous pouvons détailler comment utiliser la mémorisation d'un mouvement et de la restauration de ce même mouvement. Comme les classes Memo s'utilisent en temps qu'une pile de type FIFO, on mémorisera donc le mouvement d'un pion via la fonction memoDepCapPion(Pion p, int dir, int pas). Ensuite, on peut encore mémoriser d'autres mouvements du moment que le nombre de mouvement mémorisé ne dépasse pas le nombre de classes Memo qui ont été initialement définies par l'utilisateur. Pour revenir sur les mouvements précédents, un simple appel à la fonction memoDefaireDepCapPion() suffira à restaurer le dernier mouvement qui est sur la pile FIFO. Ensuite, le programme dépilera la pile et nous pourrons alors avoir le choix d'empiler un nouveau mouvement ou bien de dépiler des mouvements précédents.

Ainsi cette structure d'enregistrement nous sera bien utile, vu que nous serions alors en accord pour faire tourner un algorithme de recherche de la meilleur solution tel que Alpha-Beta ou Min-Max. Le programme sauvegardera alors au maximum une branche de l'arbre généré par Alpha-Beta ou Min-Max.

Interfaçage du programme avec le Client de jeu

Pour relier notre jeu avec l'interface client, nous avons mis en place un programme intermédiaire qui permet de faire le lien, qui est le package Partie. Nous avons cette fois ci ré-établi un nouveau diagramme UML pour savoir comment ce package peut fonctionner.

Le package 'Partie' est le package qui permet de lancer des parties de la manière suivante :

• Une partie locale, en lançant le main() de la classe Partie.Partie.
• Une partie en réseau qui est reliée à l'interface client (Le package Tablut).

Pour lancer une partie réseau, on démarre le serveur de jeu en lançant le main() de Tablut.ServeurJeu puis on démarre deux Clients qui seront les joueurs qui vont jouer la partie. On peut alors par exemple faire une partie Réseau entre le joueur aléatoire définit dans le package Tablut.ClientJeu, en passant en argument la classe JoueurAleatoire, et notre joueur aléatoire de notre jeu Tablut.ClientJeu, en passant en argument JoueurProjetIA qui est relié avec la classe Partie.Partie.

Le package 'Partie' permet donc de lancer des parties en se servant du Package 'Jeu'. Mais ce package permet aussi de définir la notion de Coup (les coups qui seront joués par les joueurs) et aussi de définir les « types d'intelligences », c'est à dire que l'on aura :

• l'intelligence humaine (Partie.agloChoixHumain)
• l'intelligence aléatoire (Partie.algoAleatoire)
• l'intelligence Alpha-Beta (Partie.algoAlphaBeta)

Implémentation de l'Intelligence Artificielle

Choix de l'algorithme :

Notation, on donne :

• l = facteur de branchement moyen du jeu
• p = profondeur de recherche dans l'arbre.

Nos objectifs étaient de coder directement un algorithme tel que Alpha-Beta, car il est largement plus rapide (de complexité l^p/2) qu'un algorithme de type Min-Max (de complexité l^p) et rend exactement les mêmes solutions. Alors nous nous n'avons pas implémenté d'algorithme de tye Min-Max.

De plus nous savions qu'il est interressant d'implanter un algorithme de type Itérative Deepening. En effet, un certain nombre de noeud seront revu plusieurs fois à chaque fois que nous lancerons un Alpha-Beta à une profondeur supplémentaire. Mais si nous considérons que le facteur de branchement, on prend le nombre de choix possible de jouer pour un joueur en considérant tous ces pions et tous les déplacements possibles des pions, qui sera en moyenne maximale (16*9 + 16 * 12)/2 = 168 (ie : 16 déplacements possibles pour un pion, sachant qu'il y a 9 pions blanc et 12 pions noirs). Et avec une profondeur p=3 on aura au total 168 + 168^2 + 168^3 = 4770024 noeuds à parcourir alors qu'un Alpha-Beta simple de p=3 aurait au total 168^3 = 4741632 noeuds. Soit 0,5% de noeuds supplémentaires. Il devient donc très avantageux d'implémenter un Itérative Deepening. Nous avons donc programmé un algorithme Itérative Deepening qui executera un Alpha-Beta à n profondeurs successives.

Un des avantages de notre structure pour l'implémentation de l'algorithme lors de l'exécution de Alpha-Beta est de pouvoir être très flexible sur le choix de l'état suivant, lorsque l'on applique la récurrence de l'algorithme. En effet, chaque pion connaît exactement, dans une direction choisie, le nombre de pas qu'il peut faire pour se déplacer. Ainsi, il est facile de choisir une branche à développer en jouant un coup plutôt qu'une autre.
Choix de l'heuristique :

Il y a deux sortes d'heuristiques lorsque le plateau est évalué :

• une heuristique qui évalue une feuille du plateau.
  En effet, un plateau est considéré comme étant une feuille de l'arbre développé par l'algorithme Alpha-Beta.Si l'un des deux joueurs à gagné la partie. C'est-à-dire si le roi a réussi à sortir ou bien si le roi s'est fait capturé. A ce moment, nous considérons que l'heuristique est maximale pour bien signifier à l'algorithme alpha-béta que l'état du plateau est critique et détermine une victoire ou bien une défaite.
  Nous pouvons ajouter que nous avions remarqué quelque chose d'important sur l'heuristique qui évalue une feuille du plateau. Nous avons vu qu'il fallait faire intervenir la profondeur d'une feuille. En effet, à profondeurs différentes, l'algorithme alpha-béta peut trouver par exemple plusieurs feuilles de victoire en parcourant l'arbre et les feuilles auront toutes la même valeur. L'algorithme alpha-béta n'aura donc pas de préférence à choisir un coup qui sera destiné à arriver à aller vers une victoire dans un nombre de coup plus important qu'un autre coup qui sera destiné à arriver à aller vers une victoire dans un nombre de coup moins important. C'est-à-dire que l'algorithme alpha-béta en pratique pourrait par exemple jouer un coup direct pour gagner la partie, mais celui-ci a vu qu'il pouvait aussi gagner la partie dans les prochains coups. Mais nous, nous aimerions bien sûr qu'il gagne directement. C'est la raison pour laquelle nous avons modifié l'heuristique des feuilles et nous donnons plus d'importance aux feuilles qui sont moins profondes que d'autres feuilles qui sont plus profondes.
• une heuristique qui évalue un plateau à une profondeur p.
  En effet, l'algorithme alpha-béta va aller jusqu'à la profondeur p pour pouvoir évaluer le plateau. A ce moment, notre heuristique choisie est égale au nombre de pions ami du plateau moins le nombre de pions ennemi du plateau.

Documentation

Le programme livré avec le code source est entièrement documenté. Chaque fonction a été commentée et décrit ses spécifications. Nous avons généré le Javadoc et vous pouvez alors consulter les détails du programme en allant dans le dossier « doc ».